Energy band structure and optical properties of boron arsenide

This paper out of the Scanlon group studies the electronic band structure and optical properties of boron arsenide using the relativistic quasiparticle self-consistent GW approach, including electron-hole interactions through solution of the Bethe-Salpeter equation. They also calculate its electronic and optical properties using standard and hybrid density functional theory. They demonstrate that the inclusion of self- consistency and vertex corrections provides substantial improvement in the calculated band features, in particular when comparing our results to previous calculations using the single-shot GW approach and various DFT methods, from which a considerable scatter in the calculated indirect and direct band gaps has been observed.

Materials that can transfer heat rapidly are essential for microelectronic components, where overheating is a key issue. As devices get ever smaller, such materials are in greater and greater demand, but the most efficient material, i.e. diamond, is very expensive and not compatible in terms of its thermal expansion with most materials used in microelectronics. Recently, boron arsenide has been shown to be able to conduct heat at a rate comparable to that of diamond, while being much cheaper and easier to incorporate in devices. It is difficult to grow single crystals of this material, however, so that it remains poorly characterised, particularly in terms of its fundamental electronic and optical properties. Although the methods they use have individually been applied to many systems, combining them has very rarely been done to date and represents the state-of-the-art.

Considering the importance of this exciting new thermal transport material, calculating its properties at this level of theory represents a significant step in understanding the fundamentals of boron arsenide.

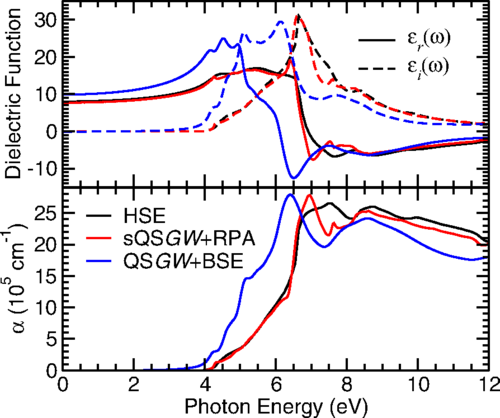
Figure shows real and imaginary parts of the dielectric function $\epsilon_r(\omega)$ and $\epsilon_i(\omega)$, calculated from hybrid DFT with the HSE functional (black lines), scaled QSGW within the random phase approximation (RPA, red lines), and via the inclusion of ladder diagrams by solution of the Bethe-Salpeter equation (BSE, blue lines). The bottom panel shows the derived optical absorption, $\alpha(\omega)$.