Examples

Metal-insulator transition in copper oxides induced by apex displacements

The Quasiparticle Self-Consistent GW approximation is combined with Dynamical Mean Field theory (DMFT). It is shown that by varying the positions of apical oxygen atoms, a metal-insulator transition can be induced in La₂CuO₄. This work also shows that optical conductivity can be well predicted by the theory and shows how spin and charge susceptibilities and the superconducting pairing order parameter, vary with the apical O displacement. QSGW+DMFT provides a new approach to handle strong correlations with predictive capability greatly superior to conventional methods such as DFT+DMFT.

In this paper, one- and two-particle properties of $\mathsf{La_2CuO_4}$ and $\mathsf{Nd_2CuO_4}$ are examined by combining the Quasiparticle Self-Consistent GW approximation (QSGW) with Dynamical Mean Field Theory (DMFT). To benchmark the method, we show that the optical conductivity is well described by QSGW+DMFT.

The paper has two main findings: first, that thanks to its superior independent-particle starting point, QSGW provides an excellent bath for DMFT. Properties such as the optical conductivity are well described, which was not possible before, e.g. DMFT embedded in a DFT bath. We show how the nonlocality in the GW self-energy plays an essential role in the electronic structure, and how the orbital character of the QSGW bands differs significantly from DFT.

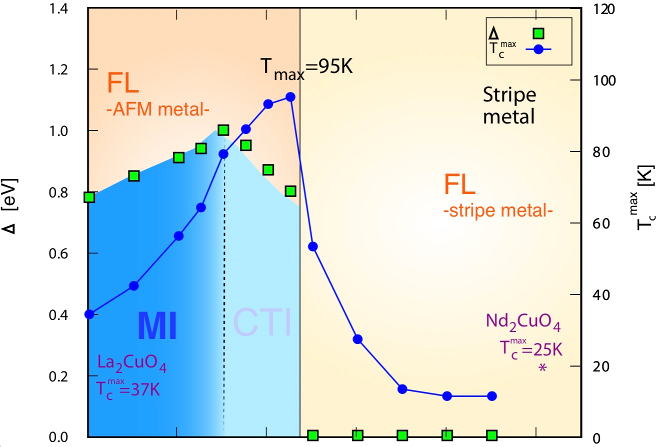
Phase diagram of LCO

This paper draws some very interesting conclusions about the origins of superconductivity in the copper oxides. It shows that the apical oxygen strongly affects the electronic structure in $\mathsf{La_2CuO_4}$ , and with suitable displacements $\mathsf{\delta}$ can a metal-insulator transition can be induced. In the Figure above the charge gap $\mathsf{\Delta}$ is shown as a function of $\mathsf{\delta}$ , together with the d-wave order parameter ( $\mathsf{T_c}$ is used as a proxy for the order parameter because these compounds are thought to be d wave superconductors).

The evolution of the two-particle response functions (charge and spin susceptibilities) are also shown. There is transition from antiferromagnetic ordering to stripe ordering near the metal-insulator transition; this is also where the pairing order parameter reaches a maximum. The Figure below shows how the spin susceptibility changes dramatically in magnitude with small displacements $\delta$ , and that the maximum point shifts from antiferromagnetic vector $\mathsf{(\pi, \pi)}$ at $\mathsf{\delta = 0}$ , to a stripe ordering $\mathsf{(\pi, 0)}$ at $\mathsf{\delta = 0.07}$ .

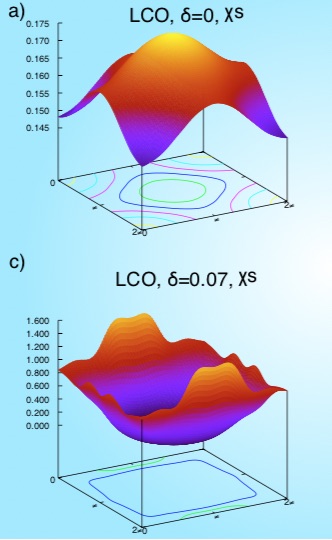
Phase diagram of LCO

This work is described in Phys. Rev. X 8, 021038.

2018-03-18 PAPERS · DMFT