Introductory QSGW Tutorial
This tutorial provides a basic demonstration of a quasi-particle self-consistent GW (QSGW) calculation. Theory for GW and QSGW, and its implementation in the Questaal suite, can be found in references 1-5.
It begins with a calculation for Si in the local-density approximation (LDA). QSGW needs a starting point and usually relies on density-functional theory for it; but importantly, the final result should not depend on the starting point in QSGW,6 in contrast to standard (often referred to as 1-shot) GW calculations do. Self-consistency not only eliminates ambiguity in the starting point, it greatly improves the systematics and fidelity of GW. It also makes it possible to trace how diagrams missing from the theory systematically improve on the result. (The tradeoff is that QSGW is considerably more expensive than 1-shot GW.) An example of a 1-shot GW calculation is provided in a separate tutorial.
After a self-consistent self-energy is obtained, the energy bands are drawn, and the macroscopic dielectric function is calculated in the random phase approximation (RPA). The calculated is repeated with the addition of ladder diagrams. Another tutorial explains how to calculate both the screened coulomb interaction and with ladder diagrams.
Self-consistent LDA calculation, and energy bands
nano init.si
blm init.si --optics --brief --nk=4 --mix~nit=20 --gw~nvbse=4~ncbse=4 --ctrl=ctrl --autobas~ehmx=-.5
lmfa si
lmf si > out.lmfsc
lmchk ctrl.si --syml~n=41~lblq:G=0,0,0,L=1/2,1/2,1/2,X=1,0,0,W=1,1/2,0,K=3/4,3/4,0~lbl=LGXWGK
lmf ctrl.si --quit=rho
lmf ctrl.si --band~fn=syml
cp bnds.si bnds.blue
lmfgwd --job=-1 si
touch meta; rm -r meta
lmgwclear si
~/lmf/speedup/lmgw.mvs.sh --maxit=0 ctrl.si > lmgw.log
Energy bands from iteration 0:
lmf ctrl.si --quit=rho
lmf ctrl.si --band~fn=syml
echo -13,10,5,10 | plbnds -fplot -ef=0 -scl=13.6 bnds.si
cp bnds.si bnds.red
fplot -f plot.plbnds
open fplot.ps
Iterating QSGW to Self-consistency:
rm -f mixm.si
~/lmf/speedup/lmgw.mvs.sh ctrl.si >> lmgw.log
lmf ctrl.si --band~fn=syml
cp bnds.si bnds.green
Combine energy bands:
echo -13,10,5,10 | plbnds -fplot -ef=0 -scl=13.6 -dat=green -lbl green
echo -13,10,5,10 | plbnds -fplot -ef=0 -scl=13.6 -dat=red -lbl red
echo -13,10,5,10 | plbnds -fplot -ef=0 -scl=13.6 -dat=blue -lbl blue
mv plot.plbnds plot.plbnds~
echo "% char0 colg=1,bold=4,clip=1,col=.3,1,.2" >>plot.plbnds
echo "% char0 colr=3,bold=4,clip=1,col=1,.2,.3" >>plot.plbnds
echo "% char0 colb=2,bold=2,clip=1,col=.2,.3,1" >>plot.plbnds
awk '{if ($1 == "-colsy") {sub("-qr","-lt {colg} -qr");sub("blue","green");print;sub("green","red");sub("colg","colr");print;sub("red","blue");sub("colr","colb");print} else {print}}' plot.plbnds~ >> plot.plbnds
fplot -f plot.plbnds
rm -r meta
~/lmf/speedup/lmgw.mvs.sh -vnkgw=8 --epsq ctrl.si
mcx -r:h5~id=freq eps.h5 -s13.6 -r:h5~z~id=eps eps.h5 -real -r:h5~z~id=eps eps.h5 -s0,-1 -real -ccat -ccat > dat.8
fplot -frme 0,.7,0,.8 -x 1.5,6 -colsy 2 dat.8 -lt 2 -colsy 3 dat.8
open fplot.ps
rm -r meta
~/lmf/speedup/lmgw.mvs.sh -vnkgw=12 --epsq ctrl.si
mcx -r:h5~id=freq eps.h5 -s13.6 -r:h5~z~id=eps eps.h5 -real -r:h5~z~id=eps eps.h5 -s0,-1 -real -ccat -ccat > dat.12
rm -r meta
~/lmf/speedup/lmgw.mvs.sh -vnkgw=16 --epsq ctrl.si
mcx -r:h5~id=freq eps.h5 -s13.6 -r:h5~z~id=eps eps.h5 -real -r:h5~z~id=eps eps.h5 -s0,-1 -real -ccat -ccat > dat.16
fplot -frme 0,.7,0,.8 -x 1.5,6 -colsy 2 dat.8 -lt 2 -colsy 3 dat.8 -lt 1,col=1,0,0 -colsy 2 dat.12 -lt 2,col=1,0,0 -colsy 3 dat.12 -lt 1,col=0,1,0 -colsy 2 dat.16 -lt 2,col=0,1,0 -colsy 3 dat.16
⟨ Reduce lcutmx in GWinput, if desired ⟩
rm -r meta
~/lmf/speedup/lmgw.sh -vnkgw=8 --epsq --bse ctrl.si > bse.log
mcx -r:h5~id=freq epsbse.h5 -s13.6 -r:h5~z~id=eps epsbse.h5 -real -r:h5~z~id=eps epsbse.h5 -s0,-1 -real -ccat -ccat > bsedat.8
fplot -frme 0,.7,0,.8 -x 1.5,6 -colsy 2 bsedat.8 -lt 2 -colsy 3 bsedat.8
rm -r meta
mn="env OMP_NUM_THREADS=4 MKL_NUM_THREADS=4 mpirun -n 4"
~/lmf/speedup/lmgw.sh -vnkgw=12 --mpirun-n "$mn" --epsq --bse ctrl.si > bse.log
Introduction
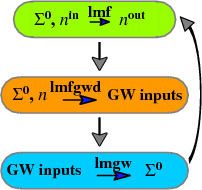
Each iteration of a QSGW calculation has two main parts: a section that uses effective one-body hamiltonians to make the density n (as in DFT; only now the generating potential does not depend on n alone), and the GW code that makes the self-energy of an interacting hamiltonian. For quasiparticle self-consistency, the GW code makes a “quasiparticlized” self-energy , which is used to construct the effective one-body hamiltonian for the next cycle. The process is iterated until the change in becomes small. Usually the interacting isn’t made explicitly, but you can do so, as explained in this tutorial. See References 1-5 for a discussion of QSGW and Questaal’s implementation of it.
In Questaal the one-body executable is lmf. The script lmfgwd is similar to lmf, but it is a driver whose purpose is to set up inputs for the GW code. is made by a shell script lmgw.sh, which runs the cycle shown in the figure above. It also does some bookkeeping, such as monitoring convergence to self-consistency. (In the classic code, lmgwsc plays the role of lmgw.sh, which is a wrapper for script lmgw that calls the relevant compiled codes.)
This tutorial also uses some auxiliary utilities, e.g. plbnds and fplot. Postscript files can be rendered by your favorite postscript viewer, here assumed for purposes of demonstration the Apple open utility.
Before any self-energy exists, it is assumed to be zero. Thus the one-body hamiltonian is usually the LDA, though it can be something else, e.g. LDA+U7. We call the cycle before exists the “zeroth iteration.”
At any step in the cycle there are two self-energies and two corresponding Green’s functions: the interacting and non-interacting . At self-consistency the poles of and coincide: this is a unique and very advantageous feature of QSGW. It means that there is no “mass renormalization” of the bandwidth — at least at the GW level. Indeed the QSGW energy bands can be wider than bands given by density-functional theory, as in Ref 8. In correlated materials, they are typically narrower; see for example Ref 9.
In short, a QSGW calculation consists of the following steps. The starting point is a self-consistent DFT calculation (usually LDA). The DFT eigenfunctions and eigenvalues are used by the GW code to construct a self-energy . This is called the “0th iteration.” If only the diagonal parts of are kept, the “0th” iteration corresponds to what is sometimes called 1-shot GW, or as GLDAWLDA.
In the next iteration, is added to the LDA hamiltonian. The density is made self-consistent, and control is handed over to the GW part. (Note that for a fixed density cancels the exchange-correlation potential from the LDA hamiltonian.) This process is repeated until the RMS change in falls below a certain tolerance value. The final self-energy (QSGW potential) can be thought of as an effective exchange-correlation functional that is tailored to the system. This is very convenient as it can now be used in an analogous way to standard DFT to calculate properties such as the band structure.
Note: The main GW algorithm has been completely redesigned by D. Pashov. It is much more efficient and makes extensive use of MPI, OPENMP, and multithreading. It has also been adapted to run efficiently on NVidia A100 and V100 GPU’s. In this tutorial we will use the current code, but also present instructions for the classic implementation.
Preliminaries
This tutorial assumes you have downloaded the repository (see this page for instructions on getting access to and downloading the Questaal package), that you have built (compiled) the executable codes and installed them in a some directory in your path, e.g. ~/bin.
The source code for all Questaal executables can be found here.
LDA calculation
The starting point is a self-consistent LDA density, and proceeds in almost the same way as the introductory DFT tutorial for silicon. The starting input is the same. Copy the following lines to file init.si):
LATTICE
# ALAT is a length scale, in atomic units
ALAT=10.26
# PLAT refers to primitive lattice vectors, in units of alat
PLAT= 0.00 0.50 0.50
0.50 0.00 0.50
0.50 0.50 0.00
# POS refers to cartesian coordinates, in units of alat
SITE
ATOM=Si POS= 0.00 0.00 0.00
ATOM=Si POS= 0.25 0.25 0.25
Run the following commands to obtain a self-consistent density:
blm init.si --optics --brief --nk=4 --mix~nit=20 --gw,nk=3 --ctrl=ctrl
lmfa si
lmf si > out.lmfsc
In contrast to the basic tutorial, blm includes an extra --gw switch, which tailors the ctrl file for a GW calculation. To see how it affects the ctrl file, try running blm without --gw. The switch modifies the basis set section (see the AUTOBAS line) to increase the size of the basis, which is necessary for GW calculations.
Two new blocks of text, the HAM and GW categories, are also added towards the end of the ctrl file. The extra parameters in the HAM category handle the inclusion of a quasiparticlized GW self-energy . The GW category provides some default values for parameters that are required in the GW calculation. The GW code has its own input file and the DFT ctrl file influences what defaults are set in it, we will come back to this later.
Note: In practice the usual LDA hamiltonian is made with a local exchange correlation potential , and is added to it. This useful because as the density changes, the change in the LDA potential , is a reasonable proxy for the change in ; thus should be smaller than .
Now check the output file out.lmfsc. It should converge in 10 iterations as can be seen from grep DQ out.lmfsc. Note that ehf and ehk should be essentially the same (-1156.140505 Ry); see the end of out.lmfsc or inspect save.si.
Look for the bandgap (grep gap out.lmfsc). It should be around 0.58 eV. Note that, because we used a coarse mesh of 4×4×4 k points, the closest conduction band minimum to the actual minimum on this mesh is at X. Thus what is printed is the gap between Γ and X, not the true minimum gap, which occurs on the Γ-X line (see this tutorial and is slightly smaller. In any case it is well below the the experimental gap (1.2 eV).
Now that we have the input eigenfunctions and eigenvalues, the next step is to carry out a GW calculation. Before moving on to the GW calculation, let’s make the LDA energy bands. lmf requires a symmetry lines file. We’ll chose the popular sequence L,Γ,X,W,ΓK (we are just tracing the same steps in the LDA tutorial). Make the symmetry-lines file this way (syml.si)
lmchk ctrl.si --syml~n=41~lblq:G=0,0,0,L=1/2,1/2,1/2,X=1,0,0,W=1,1/2,0,K=3/4,3/4,0~lbl=LGXWGK
Aside: If you need to see or remember what a particular command-line switch does, you can either run the executable with --h, which supplies minimal information, or see the command-line arguments web page For the --syml switch this documentation just points to another page where it is explained in more detail.
Make the bands as follows:
lmf ctrl.si --quit=rho ← makes a pass without changing the density: sets the Fermi level
lmf ctrl.si --band~fn=syml
cp bnds.si bnds.blue ← save it so we can compare to GW
To view the LDA bands, see this tutorial. For now we’ll defer drawing figures until we have GW results to compare with.
How lmf incorporates GW self-energies
lmf is code that implements density functional theory. But it also can read a (quasiparticlized) self-energy (more accurately, ), which it adds to the . With this addition most of the functions performed at the LDA level can also be performed at the QSGW level.
The GW scheme computes in the band representation, i.e. as . can also be rotated to the orbital basis, . In Questaal’s basis set, basis functions are centered at some site in the unit cell, and each site has multiple orbitals, labelled . is stored on disk in this representation (file sigm.ext).
The GW code must calculate at specific k points; however, lmf has a very handy scheme to interpolate to any k. Roughly speaking, is inverse Bloch transformed to a real-space form, . can be evaluated for any k by a forward Bloch transform of at the desired k. The real algorithm is somewhat more complicated, but this is the main idea. This facility is extremely useful: it is possible to put the QSGW potential on the same footing as a density-functional potential — able to generate energy bands or other properties on an arbitrary mesh.
Note: the k-mesh for (read from GW_NKABC) is distinct from the k mesh lmf uses for Brillouin zone integrations (read from BZ_NKABC). This is possible to do because of the interpolation scheme just noted. Typically a coarser mesh can often be used for because it varies more smoothly than the rest of the hamiltonian (kinetic energy especially). For that reason it is not necessary to evaluate on as fine a k mesh as lmf requires, e.g. to make Brillouin zone integrations for the density-of-states or the charge density. This is fortunate because the work needed to generate is much greater than the work lmf needs to generate the rest of the hamiltonian. (In the existing implementation the computation time to make scales as (number-of-k-points)2). Through the relation between real- and reciprocal- space representations of , it is apparent that the number of k points needed for in k space is related to the range of in real space.
This tutorial selected a k mesh of 3×3×3 divisions on which make and the self-energy, . This mesh is a bit rough, but it makes the calculation fast and for Si the results are reasonable. In this tutorial we will stick with 3 k divisions, but you need to monitor the k convergence. This can be time consuming and unfortunately there are no shortcuts.
GW_GCUTX controls the plane wave cutoff of the two-particle basis. The computational cost is sensitive to this value, so you want to make it as low as possible without messing up the results. It is a good idea to try a couple of values to satisfy yourself that you have made a sensible choice: make it as small as you can while keeping the QP levels reasonable well converged.
In correlated cases the mixing parameter beta for the self-energy, analogous to the mixing parameter beta for the charge density, that controls how much of the current iteration is to be admixed with prior ones, need to be reduced. It is controlled by GW_MIXBETA.
Other convergence parameters to particularly watch out for are the product basis tolerance, the augmentation lcutmx, and whether product basis functions are included for shallow core states. The GWinput file is documented on this page.
Running QSGW
We are now ready for a QSGW calculation, which you do with the shell script lmgw.sh: further documentation for lmgw.sh can be found on this page.
lmgwclear si
lmgw.sh --maxit 2 ctrl.si
For the classic code, use lmfgwd compiled with the classic to make GWinput. Then do
lmgwsc --wt --insul=4 --tol=2e-5 --maxit=0 si &larrr; zeroth iteration of QSGW calculation
Switch ‘–wt’ includes additional timing information in the printed output, insul refers to the number of occupied bands (normally spin degenerate so half the number of electrons), tol is the tolerance for the RMS change in the self-energy between iterations and maxit is the maximum number of QSGW iterations. Note that maxit is zero, this specifies that a single iteration is to be carried out starting from DFT with no self-energy (zeroth iteration).
Take a look at the line containing the file name llmf:
lmgw 14:14:45 : invoking mpirun -n 1 lmf --no-iactive si >llmf
Each QSGW iteration begins with a self-consistent DFT calculation by calling the program lmf and writing the output to the file llmf. We are starting from a self-consistent LDA density (we already ran lmf above) so this step is not actually necessary here. The next few lines are preparatory steps. The main GW calculation begins on the line containing the file name ‘lbasC’:
lmgw 14:15:37 : invoking mpirun -n 1 rdata4gw_v2 --job=0 --legacy=0 >lrdata4gw
lmgw 14:15:37 : invoking mpirun -n 1 heftet --job=1 >leftet
lmgw 14:15:37 : invoking mpirun -n 1 hchknw --job=1 >lchknw
lmgw 14:15:38 : invoking mpirun -n 1 hbasfp0 --job=3 >lbasC
lmgw 14:15:38 : invoking mpirun -n 1 hvccfp0 --job=0 >lvccC ... 0.0m (0.0h)
lmgw 14:15:40 : invoking mpirun -n 1 hsfp0_sc --legacy=0 --job=3 >lsxC ... 0.0m (0.0h)
lmgw 14:15:40 : invoking mpirun -n 1 hbasfp0 --job=0 >lbas
lmgw 14:15:41 : invoking mpirun -n 1 hvccfp0 --job=0 >lvcc ... 0.0m (0.0h)
lmgw 14:15:43 : invoking mpirun -n 1 hsfp0_sc --legacy=0 --job=1 >lsx ... 0.0m (0.0h)
lmgw 14:15:43 : invoking mpirun -n 1 hx0fp0_sc --job=11 >lx0 ... 0.1m (0.0h)
lmgw 14:15:47 : invoking mpirun -n 1 hsfp0_sc --legacy=0 --job=2 >lsc ... 0.1m (0.0h)
lmgw 14:15:53 : invoking mpirun -n 1 hqpe_sc --legacy=0 4 >lqpe ... 0.0m (0.0h)
The three lines with lbasC, lvccC and lsxC are the steps that calculate the core contributions to the self-energy and the following lines up to the one with lsc are for the valence contribution to the self-energy. The lsc step, calculating the correlation part of the self-energy, is usually the most expensive step.
The last step (hpqe_sc) collects terms to make quasiparticlized self-energy and writes it to file sigm for every irreducible k point. Further information can be found in the annotated GW output page.
It is interesting to compare one-shot results from the 0th iteration to the output of lmgw1-shot.
The self-energy produced so far is essentially the same as GLDAWLDA generated in the one-shot tutorial, only now there is no Z factor and the full is generated. This is distinct from computing the level shift in first=order perturbation theory as lmgw1-shot did (and most GW codes do). This requires only the diagonal , which is faster and easier to make (and is why QSGW is more expensive to do).
Even though it is standard practice to use a Z factor in 1-shot GW, in the Appendix of reference 1 we explain why it is better to use Z=1 even in the 1-shot case. (It is a poor man’s version of self-consistency.) Finally, in the self-consistent case the Z factor makes no sense because the input and output quasiparticle levels are the same.
Inspect the output of lmgw.sh
recording execution environment to file env
16:57:57 env > env
starting iteration 1 of 2
16:57:57 lmfgwd --job=0 --lmqp~rdgwin --gwcode=2 --no-iactive ctrl.si &> llmfgw00 ← Makes some setup files, e.g. the list of k points
16:57:57 lmfgwd --job=1 --gwcode=2 --no-iactive ctrl.si &> llmfgw01 ... 1s ← Makes eigenfunctions and some matrix elements for GW
16:57:58 rdata4gw_v2 --job=0 --efmode=1 --chknwmode=1 ctrl.si &> lrdata4gw ← Translates some files into formats the GW recognizes
16:57:58 hbasfp0 --job=3 --ppbfl=ppbrdc.h5 ctrl.si &> lbasC ← Makes the product basis for the core partial waves
16:57:58 hbasfp0 --job=0 ctrl.si &> lbas ... 1s ← Makes the product basis for the valence partial waves
16:57:59 hvccfp0 --ppbfl=ppbrdc.h5 --vcfl=vcc.h5 ctrl.si &> lvccC ... 1s ← Makes the Hartree potential for the core
16:58:00 hvccfp0 ctrl.si &> lvcc ... 1s ← Makes matrix elements of the Hartree potential
16:58:01 hsfp0_sc ctrl.si &> lsxC ← Makes the Hartree-Fock exchange potential for the core
16:58:01 lmsig ctrl.si &> lsg ... 6s ← Makes the self-energy and writes Sigma0
... rms change in sigma: 1.11e-3, tol: 1e-5. ← Prints the RMS change in Sigma0 from prior iteration
16:58:07 rm -f mixm.si
16:58:07 lmf ctrl.si &> llmf ... 1s ← Makes the density self-consistent for an updated Sigma0
16:58:08 save_iter "1run" "llmf llmfgw_0 llmfgw00 llmfgw01 llmfgw02 llmf02 lrdata4gw lbasC lvccC lsxC lbas lvcc lx0 lw0 lbsw-b* lbse lsg lqpe sig.h5 sigm sigm.si beff.si bnds.si save.si rst.si ctrl.si site.si basp.si atm.si GWinput switches-for-lm bse-flags lmsig-flags tol c4tol c4maxit maxit"
lmgw: iter 1 of 1 completed in 11s, 11s from start. RMS change in sigma = 1.11e-3 Tol = 1e-5 more=F
Note the last step: lmf was invoked to make a new charge density in the presence of a fixed . In the absence of self-consistency, there is an ambiguity as to whether the original density or the updated one should be used to interpret results. (If only the diagonal part of is retained, as is usual in 1-shot calculations, the addition of doesn’t change the density: only the QP levels change).
Inspect llmf to see what effect the addition of has
The following line specifies that the GW potential is being used:
RDSIGM: read file sigm and create COMPLEX sigma(R) by FT ...
The GW potential is automatically added if sigm.si is present, provided the HAM_RDSIG tag in the ctrl file is set appropriately
Near the end of the first iteration you should find the following
mixrho: sought 2 iter, 3182 elts from file mixm; read 0. RMS DQ=6.65e-4
RMS DQ is small, which says that the GW eigenfunctions and the LDA eigenfunctions are very similar. This is true for Si and other simple sp semiconductors. It explains why traditional 1-shot calculations in such systems have been successful. The situation becomes very different when correlations are no longer weak.
You can also see the bandgap:
VBmax = 0.160399 CBmin = 0.252678 gap = 0.092278 Ry = 1.25499 eV
...
VBmax = 0.159132 CBmin = 0.253739 gap = 0.094607 Ry = 1.28665 eV
The first line is the GW gap generated from the LDA density; the second reflects the effect of updating the density to self-consistency. This can be expressed as a change , where is implicitly given through self-consistency in the lmf cycle.
Both are similar (reflecting once again that the density is minimally affected) and quite close to the experimental gap.
Before continuing, let’s make and preserve the energy bands from the 0th iteration.
lmf ctrl.si --quit=rho # makes a pass without changing the density: sets Ef in moms.si
lmf ctrl.si --band~fn=syml
cp bnds.si bnds.red # save it so we can compare to other bands
Iterating QSGW to self-consistency, preliminary considerations
Remarks regarding iterations to self-consistency:
You can skip this section you just want to get on with the tutorial. However, the points below are important things to keep in mind if you want to make the best use of lmgw.sh.
As it executes, lmgw.sh records the iteration it is in and whatever instruction it executes wthin that iteration. Thus, if a calculation is aborted it can restart where the last calculation left off. This information is in directory meta. Inspect the directory (
ls meta/) and you will find only one file, meta/iter. Once all the intermediate steps of an iteration are completed, meta is cleared except for the iterations counter (the contents of meta/iter should be 1 for now). If you don’t want lmgw.sh to remember its history, simply remove this directory.Two self-energy files are present, sigm.si and sig.h5. Eventually these will be merged into one file, but for now, note that sig.h5 is used by lmgw.sh and sigm.si is written only at the end of the cycle, to maintain compatibility with lmf. The two files are now in sync, so it doesn’t matter in the present case; however if you start from a directory containing only the sigm file, you should make a corresponding sig.h5. Do this with:
ln -s sigm.si sigm; s2s5; rm sigm. (Having sig.h5 is only important at the end of the cycle, when self-energies are mixed).If you did not start the calculation from a fresh directory, you should remove all files *.h5 except retain or remake sig.h5.
This tutorial runs quickly, so parallelization is not needed. But lmgw.sh enables a high degree of parallelization, and you will need to make use of it when running larger calculations.
Iterating QSGW to self-consistency
Rerun lmgw.sh, this time not restricting the number of iterations
rm -f mixm.si
m1="env OMP_NUM_THREADS=16 MKL_NUM_THREADS=16 mpirun -n 1"
mn="env OMP_NUM_THREADS=4 MKL_NUM_THREADS=4 mpirun -n 4"
lmgw.sh --incount --mpirun-1 "$m1" --mpirun-n "$mn" --tol=2e-5 ctrl.si &> lmgw.log &
Inspect lmgw.log (grep RMS lmgw.log) to monitor convergence to self-consistency
lmgw: iter 2 of 100 completed in 7s, 7s from start. RMS change in sigma = 1.98e-4 Tol = 2e-5 more=T
lmgw: iter 3 of 100 completed in 6s, 13s from start. RMS change in sigma = 3.58e-5 Tol = 2e-5 more=T
lmgw: iter 4 of 100 completed in 7s, 20s from start. RMS change in sigma = 6.37e-6 Tol = 2e-5 more=F
The RMS change in rapidly dropped to a small number. We have reached self-consistency in . Look also at the RMS change in the density at the last iteration. You should see that the is essentially identical to from the prior iteration (grep RMS ./?run/llmf)
./0run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 0. RMS DQ=2.96e-6
./0run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 1. RMS DQ=2.23e-6 last it=2.96e-6
./1run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 0. RMS DQ=7.60e-4
./1run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 1. RMS DQ=5.16e-4 last it=7.60e-4
./1run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 2. RMS DQ=2.59e-5 last it=5.16e-4
./1run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 3. RMS DQ=1.92e-5 last it=2.59e-5
./2run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 0. RMS DQ=5.33e-5
./2run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 1. RMS DQ=2.93e-5 last it=5.33e-5
./3run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 0. RMS DQ=1.53e-5
./3run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 1. RMS DQ=9.97e-6 last it=1.53e-5
./4run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 0. RMS DQ=1.15e-6
./4run/llmf: mixrho: sought 2 iter, 4070 elts from file mixm; read 1. RMS DQ=8.01e-7 last it=1.15e-6
Thus at self-consistency, both and the density stop changing, ameliorating ambiguity in, e.g. the Fermi level. QSGW is not a conserving approximation as fully self-consistent GW is, but it is fairly close to a conserving one, and indeed it vastly better than one-shot GW. Morever, QSGW can provide very useful ground state properties, e.g. the charge density. Charges and magnetic moments are generally not accessible in standard GLDAWLDA.
Check the band gap evolution during the different iterations (grep gap ./?run/llmf)
./0run/llmf: VBmax = 0.162578 CBmin = 0.205082 gap = 0.042504 Ry = 0.57830 eV
./1run/llmf: VBmax = 0.160540 CBmin = 0.252664 gap = 0.092125 Ry = 1.25342 eV
./1run/llmf: VBmax = 0.160540 CBmin = 0.252664 gap = 0.092125 Ry = 1.25342 eV
./1run/llmf: VBmax = 0.160267 CBmin = 0.252883 gap = 0.092615 Ry = 1.26009 eV
./1run/llmf: VBmax = 0.160267 CBmin = 0.252883 gap = 0.092615 Ry = 1.26009 eV
./1run/llmf: VBmax = 0.159670 CBmin = 0.253378 gap = 0.093709 Ry = 1.27497 eV
./1run/llmf: VBmax = 0.159670 CBmin = 0.253378 gap = 0.093709 Ry = 1.27497 eV
./1run/llmf: VBmax = 0.159650 CBmin = 0.253433 gap = 0.093784 Ry = 1.27599 eV
./1run/llmf: VBmax = 0.159650 CBmin = 0.253433 gap = 0.093784 Ry = 1.27599 eV
./2run/llmf: VBmax = 0.159700 CBmin = 0.257482 gap = 0.097782 Ry = 1.33040 eV
./2run/llmf: VBmax = 0.159700 CBmin = 0.257482 gap = 0.097782 Ry = 1.33040 eV
./2run/llmf: VBmax = 0.159669 CBmin = 0.257512 gap = 0.097843 Ry = 1.33122 eV
./2run/llmf: VBmax = 0.159669 CBmin = 0.257512 gap = 0.097843 Ry = 1.33122 eV
./3run/llmf: VBmax = 0.158704 CBmin = 0.258781 gap = 0.100077 Ry = 1.36162 eV
./3run/llmf: VBmax = 0.158704 CBmin = 0.258781 gap = 0.100077 Ry = 1.36162 eV
./3run/llmf: VBmax = 0.158708 CBmin = 0.258753 gap = 0.100045 Ry = 1.36118 eV
./3run/llmf: VBmax = 0.158708 CBmin = 0.258753 gap = 0.100045 Ry = 1.36118 eV
./4run/llmf: VBmax = 0.158589 CBmin = 0.258881 gap = 0.100292 Ry = 1.36454 eV
./4run/llmf: VBmax = 0.158589 CBmin = 0.258881 gap = 0.100292 Ry = 1.36454 eV
./4run/llmf: VBmax = 0.158589 CBmin = 0.258874 gap = 0.100286 Ry = 1.36445 eV
./4run/llmf: VBmax = 0.158589 CBmin = 0.258874 gap = 0.100286 Ry = 1.36445 eV
Run lmgwsc again but this time without restricting the number of iterations
lmgwsc --wt --insul=4 --tol=2e-5 si
The iteration count starts from 1 since we are now starting with a self-energy from the zeroth iteration. Again, the iteration starts with a self-consistent DFT-like calculation, but now from zeroth iteration is added. Take a look at the GW output again and you can see that the rest of the steps are the same as before. After 3 iterations the RMS change in the self-energy is below the tolerance - the calculation is converged.
lmgwsc : iter 3 of 5 RMS change in sigma = 5.14E-06 Tolerance = 2e-5 more=F Mon 21 May 2018 19:08:21 BST elapsed wall time 5.0m (0.1h)
Thus at self-consistency, Σ and the density both stop changing, ameliorating ambiguity in, e.g. the Fermi level. While QSGW is not a conserving approximation, it is fairly close to a conserving one, and indeed vastly better than one-shot GW. This points out one very useful ground state property QSGW can give you: the density. It can also give you spin densities, e.g. magnetic moments.
Inspect llmf (output of lmf in the last cycle) and you can find that the gap is now around 1.38 eV (grep gap llmf). It is larger because the one-body hamiltonian generating has a wider gap, which which increases and thus .
Note: a carefully converged calculation should yield a gap of about 1.23 eV.
Make the bands a third time so we can compare LDA, GW(iteration 0), and QSGW.
rm -r mixm.si
lmf ctrl.si --quit=rho ← makes a pass without changing the density: sets Fermi level in moms.si
lmf ctrl.si --band~fn=syml
cp bnds.si bnds.green ← save it to compare with other bands
Check your directory and you will see that a number of intermediate files were created, that are no longer needed. The following command removes many redundant files:
lmgwclear
Further details can be found in the Additional exercises below.
QSGW energy bands
As noted previously, lmf has a very powerful feature, that it can takes the inverse Bloch transform to put in real space, from the mesh of points it is calculated on. Then it can interpolate to any by performing a forward Bloch transform. The details are rather complicated, but they are explained in some detail in Section IIG of PRB76, 165106.
This feature enables us to compute the energy bands and any k, and allows us to draw the energy bands with minimal effort. In fact, the energy bands have already been made and preserved in files bnds.blue (LDA), bnds.red (iteration 0) bnds.green (QSGW).
We can readily translate the bands into picture using a combination of the plbnds utility and fplot utility. Of course there are many ways to skin this cat and you may have a preferred method.
The following render the three energy bands files into the standard Questaal format for 2D arrays, which fplot can read.
echo -13,10,5,10 | plbnds -fplot -ef=0 -scl=13.6 -dat=green -lbl green
echo -13,10,5,10 | plbnds -fplot -ef=0 -scl=13.6 -dat=red -lbl red
echo -13,10,5,10 | plbnds -fplot -ef=0 -scl=13.6 -dat=blue -lbl blue
plbnds also makes a script plot.plbnds which tells fplot how to build the figure.
We’d like to plot all three bands on the same figure. To do this, modify plot.plbnds as follows:
mv plot.plbnds plot.plbnds~
echo "% char0 colg=1,bold=4,clip=1,col=.3,1,.2" >>plot.plbnds
echo "% char0 colr=3,bold=4,clip=1,col=1,.2,.3" >>plot.plbnds
echo "% char0 colb=2,bold=2,clip=1,col=.2,.3,1" >>plot.plbnds
awk '{if ($1 == "-colsy") {sub("-qr","-lt {colg} -qr");sub("blue","green");print;sub("green","red");sub("colg","colr");print;sub("red","blue");sub("colr","colb");print} else {print}}' plot.plbnds~ >> plot.plbnds
These steps modify plot.plbnds so that it will plot all three families of bands. Now do fplot -f plot.plbnds and use your favorite postscript viewer (e.g. open/okular/evince fplot.ps) to see a picture.
Your postscript file should look like the figure below.
Notes:
- Blue curves are the LDA bands
- Red curves are the 0th-iteration QSGW bands, akin to GLDAWLDA, as described in the tutorial
- Green curves are the self consistent QSGW bands.
Red and green are very similar, showing that self-consistency has a small effect in Si.
QSGW RPA dielectric function
Here we show how to calculate the macroscopic dielectric function for Si in the RPA. Another tutorial shows how to calculate the macroscopic dielectric function with ladder diagrams.
The RPA dielectric function is computed from a starting hamiltonian . You can use any available , e.g. LDA, Here we use the QSGW generated in the previous section.
The RPA dielectric function can be compute at any finite q. As of this writing, it can only approximately compute the macroscopic dielectric function, i.e. , which must be calculated at q=0 11. To well approximate we can choose a finite q very close to zero. q cannot be chosen too small, because of cancelling diverges there which are difficult to control, but we can choose a collection of small q and see how depends on the choice. The q you wish to calculate for are entered in the GW category of ctrl.si.
In this tutorial we choose q=(0,0,0.0015). Uncomment this line in ctrl.si:
# epsq=0,0,.0015 delre=.001 .1
It specifies one q near zero along the z axis (in cubic symmetry there is no direction dependence of the approach to q=0), and it also specifies a finer frequency mesh spacing than the one used for the self-consistent cycle.
Also, because takes an average over the unit cell, its detailed shape inside the unit cell is not so important. You can reduce the cutoffs significantly with minimal change in . Reducing it to 2 makes negligible difference in this case. Changes values 4 in these lines in GWinput to 2:
lcutmx(atom) = l-cutoff for the product basis
2 2
Now we are ready to compute the dielectric function. A good description of requires many more q points to get a converged answer than is needed for self-consistency. Let’s start with an 8×8×8 mesh at first. Run the calculation with
rm -r meta
~/lmf/speedup/lmgw.mvs.sh -vnkgw=8 --epsq ctrl.si
Remark: the first line is needed to remove memory of what it did in the last calculation. is written to file eps.h5. Inspect this file (h5ls eps.h5) and you should see:
eps Dataset {1, 673}
eps_nlfc Dataset {1, 673}
freq Dataset {673}
nfreq Dataset {1}
nq Dataset {1}
q Dataset {1, 3}
has been generated for 673 frequencies. Look at the individual frequencies (h5dump -d freq eps.h5, or prettier, use mcx -r:h5~id=freq eps.h5) and you should see that they range from 0 to almost 6 Ry.
You can use your favorite utilities to draw a figure; here we will use standard utilities available in Questaal, the mcx calculator and the fplot utility. This line
mcx -r:h5~id=freq eps.h5 -s13.6 -r:h5~z~id=eps eps.h5 -real -r:h5~z~id=eps eps.h5 -s0,-1 -real -ccat -ccat > dat.8
creates a file dat.8 with 673 rows and three columns () Note is converted to eV: eps.h5%freq are stored in Ry units. Draw a picture with (real part solid line, imaginary part dashed line) with
fplot -frme 0,.7,0,.8 -x 1.5,6 -colsy 2 dat.8 -lt 2 -colsy 3 dat.8
open fplot.ps
Your postscript file should look like the figure below.
Solid line: ; Dashed line: . Abscissa is frequency, in eV.
Compare to Fig 3 in the classic work of Aspnes and Studna.
The main features of the experimental dielectric function are reproduced, but there are some differences. Several observations are in order:
In the RPA, there is a sharp turn-on at around 3.4 eV. In the measured function, there is a sharp shoulder around 3.3 eV, but the transition is not abrupt. This is because Si is an indirect gap semiconductor, with a bandgap of about 1.2 eV. It does absorb between 1.2 eV and 3.3 eV, but only weakly because this transition requires a phonon assist. Our treatment does not take into account electron-phonon effects. Such have effects have been incorporated in a GW framework, see e.g. this paper. where the electron-phonon matrix element is explicitly calculated and coupled with the optical response. It can also be done with supercells, including lattice disorder stochastically, as was first done in this paper The latter does not require explicit calculation and can readily be done in a QSGW framework.
, or (more precisely, small enough to be essentially zero from the point of view of electron response but large enough to avoid nuclear contributions to the static polarizability), is known to be 11.7 at 0K. From the first row of dat.8 we obtain . This is 84% of the experimental value, and follows the well known ‘80% rule’ : . This empirical relation appears universally in QSGW, and it applies to both weakly and rather strongly correlated materials such as NiO. See for example, Figure 1 in this paper. It was studied in some detail by Kotani and coworkers and largely ameliorates the gap error in weakly and moderately correlated subsystems. The physical origin is also understood: see next point.
The shoulder above 3.4 eV rises much more slowly than the experiment, and also the strong second peak appearing at 4.7 eV is blue shifted compared to the experiment, where it occurs at about 4.3 eV. This blue shift has long been known, it was first resolved by Rohlfing and Louie, and independently by Albrecht et al around the same time. Both groups added ladder diagrams to the RPA polarizability; this has been very successful and is known to be necessary for the response function to be well described.
In Si, the effect of local fields is not very strong. If the matrix structure of is neglected, the elment can be considered a scalar and its inverse is . To extract neglecting local fields, do
mcx -r:h5~id=freq eps.h5 -s13.6 -r:h5~z~id=eps_nlfc eps.h5 -real -r:h5~z~id=eps_nlfc eps.h5 -s0,-1 -real -ccat -ccat > dat.8xDraw a picture comparing dat.8 and dat.8x. You should see that they are nearly identical.
Next we need consider the convergence in with respect to the k mesh. Repeat the dielectric calculation with 12×12×12 divisions.
rm -r meta
~/lmf/speedup/lmgw.mvs.sh -vnkgw=12 --epsq ctrl.si
mcx -r:h5~id=freq eps.h5 -s13.6 -r:h5~z~id=eps eps.h5 -real -r:h5~z~id=eps eps.h5 -s0,-1 -real -ccat -ccat > dat.12
and again with 16×16×16 divisions.
orm -r meta
~/lmf/speedup/lmgw.mvs.sh -vnkgw=16 --epsq ctrl.si
mcx -r:h5~id=freq eps.h5 -s13.6 -r:h5~z~id=eps eps.h5 -real -r:h5~z~id=eps eps.h5 -s0,-1 -real -ccat -ccat > dat.16
Use your favorite utility to draw a figure comparing the three. This fplot command will make fplot.ps:
fplot -frme 0,.7,0,.8 -x 1.5,6 -colsy 2 dat.8 -lt 2 -colsy 3 dat.8 -lt 1,col=1,0,0 -colsy 2 dat.12 -lt 2,col=1,0,0 -colsy 3 dat.12 -lt 1,col=0,1,0 -colsy 2 dat.16 -lt 2,col=0,1,0 -colsy 3 dat.16
Your postscript file should look like the figure below.
Black, red, and green correspond to 8, 12, 16 k divisions on each axis.
The overall structure is similar, but the peak in Imε becomes stronger — now somewhat larger than the experiment. Note the small peak just above 3.3 eV disappears; this peak is of excitonic origin, which is missing in the RPA.
To make a good dielectric function it is necessary to modify GWinput a little.
The 4×4×4 k mesh used for QSGW is reasonably sufficient for k integrated properties, but it is not not sufficient to pick up the detailed structure of the macroscopic dielectric function. Edit the n1n2n3 tag and increase the k mesh to 16×16×16 divisions:
n1n2n3 16 16 16 ! for GW BZ meshFor a good frequency resolution, shrink the frequency mesh spacing to dw to 0.001 Hartree (or smaller, if desired)
dw 0.001 ! mesh spacing along Real axis (Hartree)The macroscopic dielectric function is . Because it takes an average over the unit cell, the detailed shape of inside the unit cell is not so important. You can reduce the cutoffs significantly with minimal change in . Reducing it to 2 makes negligible difference in this case:
lcutmx(atom) = l-cutoff for the product basis 2 2Supply GWinput with the q points for which you want to calculate . The code does not have the ability to take the limit analytically; you must choose a finite but small q. At the end of GWinput there are the following lines
QforEPSIBZ off <QforEPS> 0d0 0d0 0.015d0 </QforEPS>
It tells the GW code to make just a one point, close to the point. This corresponds approximately to . If you want to calculate also, add a line 0.015d0 0d0 0d0. Si is cubic and , so it is not necessary here.
You can either calculate the proper macroscopic dielectric function, , or one that neglects local fields, .
The latter is must faster, but it is approximate. Often the difference between the two is not large, however. Do one of:
$ lmgw --eps --ht si
$ lmgw --epsNLF --ht si
The latter writes a file EPS0001.nlfc.dat, while the former writes both that file and EPS0001.dat.
Th first few lines should like the following
q(1:3) w(Ry) eps epsi --- LFC included.
0.00000000 0.00000000 0.01500000 0.0000D+00 0.928993543761226D+01 0.726517122804292D-15 0.107643374565477D+00 -0.841822371139706D-17
0.00000000 0.00000000 0.01500000 0.1005D-02 0.928999688792784D+01 0.721333610616975D-15 0.107642662539476D+00 -0.835805128491751D-17
0.00000000 0.00000000 0.01500000 0.3025D-02 0.929049220411353D+01 0.727839656503130D-15 0.107636923645147D+00 -0.843253724471668D-17
0.00000000 0.00000000 0.01500000 0.5065D-02 0.929149658090234D+01 0.730784249155761D-15 0.107625288487475D+00 -0.846482210402463D-17
Columns 1-4 are the q-point and frequency, respectively. Columns 5-6 are the real and imaginary parts of ; columns 7-8 are the real and imaginary parts of .
Note that even while Si has a fundamental gap of approximately 1.2 eV, it is an indirect gap semiconductor. Since the electron-phonon interaction is missing absorption from indirect transitions is not included and is zero until the first direct gap transition at 0.2516D Ry, or 3.42 eV.
You can read the static dielectric constant, from EPS0001.dat. The calculated value is 9.3, which is 79% of the actual (11.7 at 0K). This error largely originates from the neglect of ladder diagrams.
Use your favorite graphics package to draw figures. To draw Re ε as a solid line and Im ε as a dotted one, do the following:
$ mcx -f1p8e20.12 -r:s=1 EPS0001.dat -coll 4,5,6 -p -coll 1 -s13.6 -tog -coll 2:nc -ccat -inc 'x1>0&x1<10' > dat.lfc # converts to standard Questaal 2D array format
$ fplot dat.lfc -coll 3 -lt 3,bold=4 dat.lfc
$ open fplot.ps
aCompare to the neglect of local fields (superpose, use blue for no local fields)
$ mcx -f1p8e20.12 -r:s=1 EPS0001.nlfc.dat -coll 4,5,6 -p -coll 1 -s13.6 -tog -coll 2:nc -ccat -inc 'x1>0&x1<10' > dat.nolfc
$ fplot dat.lfc -coll 3 -lt 3,bold=4 dat.lfc -lt 1,col=0,0,1 dat.nolfc -coll 3 -lt 3,bold=4,col=0,0,1 dat.nolfc
You should see that the omission of local fields has a modest effect.
QSGW BSE dielectric function
As the previous section noted, excitonic effects are important. Here we use the same QSGW potential computed in RPA, but now include ladder diagrams to observe its effect on .
Remarks:
The BSE is much more complex than the RPA. We make the usual assumption that W used to construct the vertex is static. This greatly simplifies the BSE equation, not least because it reduces the BSE to a two-particle hamiltonian that couples every band to every other one (in practice we must limit the number to keep the cost manageable), and also coupling states at every q to every other q. The result are the (discrete) eigenvalues of the two-particle hamiltonian (the corresponding eigenfunctions which contain information about the spatial structure of the states).
Formally, q is continuous and the resulting spectrum is also. But we are limited to a discrete set of q, and the result the hamiltonian yields a set of discrete levels. These must be smoothed to render a reasonable-lookng figure. This is done by broadening each sharp level into a gaussian. You can specify the gaussian width through the tag GW_BSE_IMW; you don’t it will just use the default. To see what the default is, do
lmfgwd --input | grep BSE_IMW. It should be 0.02 Ry, which is a bit large. We will use 0.01 Ry.must be taken in the q→0 limit, as in the RPA case.11 The BSE code can do this with approximations to the velocity operator. It also has the ability to compute optics any any q on the mesh used in the self-consistency cycle, including the offset-Gamma points. (lmgw.sh does this when invoked with the combination
--epsq --bse). Offset Gamma points are close to q=0 and it is what we will do here.The BSE is much more expensive than the RPA. Provided we don’t use too many k points we can still get away with doing calculations in serial mode. For the BSE, we use only a few bands near the Fermi level to couple electron-hole pairs. You have to tell the code how many to use, and we will use 4 valence and 4 conduction bands in this tutorial.
Add a tag bse to the gw category in ctrl.si, like this:
gw # Parameters for GW
epsq=0,0,.0015 delre=.001 .1
nkabc={nkgw} gcutb={gcutb} gcutx={gcutx}
bse[nv=4 nc=4 imw=.01,.01]
The calculation proceeds just as in the RPA case, except for the additional --bse switch
rm -r meta
~/lmf/speedup/lmgw.sh -vnkgw=8 --epsq --bse ctrl.si
cp epsbse.h5 epsbse.nk8.h5
Now the dielectric function is stored in epsbse.h5. (The last line is there only if you want to preserve the file.)
Extract the dielectric function as in the RPA case and draw a picture
mcx -r:h5~id=freq epsbse.h5 -s13.6 -r:h5~z~id=eps epsbse.h5 -real -r:h5~z~id=eps epsbse.h5 -s0,-1 -real -ccat -ccat > bsedat.8
fplot -frme 0,.7,0,.8 -x 1.5,6 -colsy 2 bsedat.8 -lt 2 -colsy 3 bsedat.8
Your postscript file should look like the figure below.
Solid line: ; Dashed line: . Abscissa is frequency, in eV.
Remarks:
The real and imaginary parts of look much improved, agreeing well with experiment up to about 4.5 eV, with peaks in close to 3.4 and 4.1 eV matching experimental positions rather well. The amplitude at the peaks are also reasonably well described: in the experiment the first and second peaks have amplitudes about 35 and 45, respectively. Above 4.5 eV the calculated response shows more structure than the experiment. Notably, the theory predicts a third peak at around 5 eV that is seen in experiment but the peak is much more washed out.
is calculated to be close to 11, a few percent smaller than the experimental value of 11.7 eV, but much improved over the RPA. The peak in occurs at about 3.3 eV, close to the experimental value, though it is a little broader than the experiment, with a peak value of 35 rather than 43.
It is possible that the offset Gamma point is too large. You can inspect it with
h5dump -d q epsbse.nk8.h5: for an 8×8×8 mesh, q=(-0.00625, 0.00625, 0.00625). You can reduce it by half by adding a tag Q0Pscale .05 at the top of GWinput. If you do this, you will see changes only a little.Note that does not drop sharply to 0 at the band edge near 3.3 eV. This is not a physical effect; it is a consequence of the smearing in the two-particle hamiltonian.
The details of will change as the k mesh becomes finer or the broadening changes. Increasing the k mesh in the BSE case can cause it to execute very slowly in scalar mode. To see the effect of increasing the density of k points, let’s repeat this calculation for a 12×12×12 mesh. To speed it up, we assume a single-node machine with 16 cores, and split it into 4 MPI processes and 4 threads for OMP or multithreaded libraries For a discussion of how to use lmgw.sh with multiple-core machines, see [this page[/tutorial/gw/hpc]. Do the following:
rm -r meta
mn="env OMP_NUM_THREADS=4 MKL_NUM_THREADS=4 mpirun -n 4"
~/lmf/speedup/lmgw.sh -vnkgw=12 --mpirun-n "$mn" --epsq --bse ctrl.si > bse.log
This calculation runs for about an hour on a standard X86 architecture. Extract the dielectric function as in the RPA case and draw a picture comparing the 8×8×8 and 12×12×12 meshes
mcx -r:h5~id=freq epsbse.h5 -s13.6 -r:h5~z~id=eps epsbse.h5 -real -r:h5~z~id=eps epsbse.h5 -s0,-1 -real -ccat -ccat > bsedat.8
fplot -frme 0,.7,0,.8 -x 1.5,6 -colsy 2 bsedat.8 -lt 2 -colsy 3 bsedat.8 -lt 1,col=1,0,0 -colsy 2 bsedat.12 -lt 2,col=1,0,0 -colsy 3 bsedat.12
Your postscript file should look like the figure below.
Solid line: ; Dashed line: . Abscissa is frequency, in eV. Black shows for 8 divisions on each axis, red 12 devisions.
The overall features remain qualitatively similar. Peak amplitudes are somewhat softer, and the structure above 4.5 eV is smoother, though some discrepanies remain with the experimental data.
The AC conductivity
The conductivity and dielectric function are related as
What has been calculated above is the dielectric function relative to the vacuum permittivity, . Taking the real part of and scaling to appropriate units,
Using
we can write
Then
Additional Exercises
1) Fundamental gap
The gap found in the tutorial is is actually the Γ-X gap; the true gap is a little smaller as can be seen by running lmf with a fine k mesh.
2) Checking convergence in QSGW with respect to the k point mesh
Test the convergence with in the QSGW self-energy respect to the k mesh by increasing to a 8 × 8 × 8 mesh.
3) Add empty spheres or floating orbitals
Note: the existing lmf basis set is a little undersized for GW calculations in open systems. The new Jigsaw Puzzle Orbital basis should surmount this problem, but until it is operational there are three ways to enhance the basis
- Add plane waves, as shown in this tutorial. You can perform 1-shot GW calculations with APWs, but not QSGW, because there is no good way to interpolate the self-energy to arbitrary k point. So it’s not a viable option here.
- Add empty spheres — artificial sites in the interstitial with Z=0.
- Add floating orbitals. These are like empty spheres, but have no augmentation radius. These add extra smooth Hankels to the basis centered at some interstitial point.
Until JPOs are available, the best is to use floating orbitals. Finding the right spot to place them is an art form, since there is no correct or unique point. the main guide is to identify points with large voids. The easiest way is to use blm’s automatic empty sphere finder. Do this by adding --findes~float to the ctrl file generator:
$ blm init.si --gmax=5 --nk=4 --nit=20 --gw --findes~float
and observe that the site file has two extra sites labelled E.
--findes usually works very well, though it can add too many of them when the voids are large and symmetry is low, and you may need to manually intervene. There are several switches that can help you make better choices in such cases; see here for a modifiers to this switch.
Also compare how ctrl.si changes. You should see an extra line:
atom=E z= 0 r= 2.221355*{(les==11)?0:1} lmx=2 lmxa=4
This line accommodates both empty spheres and floating orbitals. If variable les is 11, R will be 0. R=0 tells lmf to treat the site as a floating orbital — a center where envelope functions will be added but with no augmentation radius. les=1 tells lmf to add a new site, an “empty” site that gets augmented like real sites. The two are similar but floating orbitals don’t have augmentation spheres, and they are preferable because they are simpler and have no effect on the GW product basis.
Repeat the tutorial with this set of (ctrl,site,basp) files, and see how much the bands change.
4) Check the effect of smearing in the BSE dielectric response.
We used a smearing of 0.01 for the BSE dielectric response. Try a smaller smearing, and a larger one, and see how the response function changes.
Footnotes and References
1 Questaal’s QSGW implementation is based on this paper:
Takao Kotani, M. van Schilfgaarde, S. V. Faleev, Quasiparticle self-consistent GW method: a basis for the independent-particle approximation, Phys. Rev. B76, 165106 (2007)
2 These papers established the initial framework for QuasiParticle Self-Consistent GW theory:
Sergey V. Faleev, Mark van Schilfgaarde, Takao Kotani, All-electron self-consistent GW approximation: Application to Si, MnO, and NiO, Phys. Rev. Lett. 93, 126406 (2004);
M. van Schilfgaarde, Takao Kotani, S. V. Faleev, Quasiparticle self-consistent GW theory, Phys. Rev. Lett. 96, 226402 (2006)
3 Questaal’s main methods paper, which includes a detailed discussion of GW and QSGW:
Dimitar Pashov, Swagata Acharya, Walter R. L. Lambrecht, Jerome Jackson, Kirill D. Belashchenko, Athanasios Chantis, Francois Jamet, Mark van Schilfgaarde, Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique, Comp. Phys. Comm. 249, 107065 (2020).
4 The first description of an all-electron GW implementation in a mixed basis set:
T. Kotani and M. van Schilfgaarde, All-electron GW approximation with the mixed basis expansion based on the full-potential LMTO method, Sol. State Comm. 121, 461 (2002).
5 An early paper of LDA-based GW based on an all-electron theory. It shows the limitations of GW based on the LDA, and the motivation for QSGW:
M. van Schilfgaarde, Takao Kotani, S. V. Faleev, Adequacy of Approximations in GW Theory, Phys. Rev. B74, 245125 (2006)
6 Metastable minima are often encountered in Hartree Fock theory and (to a lesser extent) in density-functional theory, i.e. there can be more than one minimum or stationary point. As a result there can be a discrete set of solutions, in QSGW as in Hartree Fock, though usually there is only one.
7 In some circumstances, e.g. to break time reversal symmetry inherent in the LDA, you need to start with LDA+U. CoO is a classic instance of this; it is also true for many systems with rare earth elements.
8 S.A. Chambers, T. Droubay, T.C. Kaspar, M. Gutowski, M. van Schilfgaarde ``Accurate Valence Band Maximum Determination for SrTiO3(001)’’ Surf. Sci. Lett. 554, 81 (2004).
9 Jan M. Tomczak, M. van Schilfgaarde, G. Kotliar, ``Many-body effects in iron pnictides and chalcogenides – non-local vs dynamic origin of effective masses,’’ Phys. Rev. Lett. 109, 237010 (2012).
10 In the classic GW code all information is taken from GWinput. To cause lmfgwd to write tags from the GW category of the ctrl file to the header section of GWinput, use lmfgwd --job=-1 --classicGWinput ctrl.si.
11 The polarizability at q=0 must be taken in the q→0 limit. It is not analytic and depends on the direction of approach to q=0. When the limit is taken, it involves matrix elements of the velocity operator, ⟨i | v | j⟩, which at present are calculated only approximately in Questaal. Questaal can calculate matrix elements of the momentum operator ⟨i | p | j⟩ when the potential is local, which is proportional to ⟨i | v | j⟩; but with a nonlocal the are not so simply related.
In the self-consistency cycle, the “offset Gamma method” is used to manage the q=0 microcell; it is explained in detail in Ref. 1. When a quantity is really needed at q=0, e.g. the macroscopic dielectric function, Questaal either approximates it with a small, but finite q (see this section for an example, or it uses an approximate form for ⟨i | v | j⟩. An exact expression for ⟨i | v | j⟩ is under development.





